【誰でも簡単】 「土方カーブ」 の計算方法と現場でスグに使える活用事例3選

本記事では、こんな悩みを解決します。

この記事では、土木の現場監督として７年間働いた私が、土方カーブの計算方法と現場での利用方法を解説します。

これを読み終えれば、現場で土方カーブを使いこなすことができるようになり、現場の管理に係る時間が減らすことができます。

執筆者

また、土方がどのように見られているか、については[土木作業員がクズと言われる理由！工事現場で７年働いた元ゼネコンマンが解説]で詳しく解説しています。

土方カーブとは？現場で簡単にカーブを出す測量の方法のこと

土方カーブというのは、単曲線の中間点を簡単に計算し、現場に再現できる方法です。
単曲線の中心点を簡単に算出できるので、光波測量器等の測量機器を使用することなく、現場で簡易的にカーブを再現することが出来ます。

では、実際に現場でどのように出していくのか、詳しく解説してます。

現場における土方カーブの使用例

起点(No.0)、終点(No.1)、中間点(No.2)の位置がわかる単曲線を例にします。

土方カーブは、単曲線上の位置がわかっている場合、その中央点を四則演算だけの簡単な計算で求められることです。

具体的には、No.0〜1(No.0+10)の中央点およびNo.1〜2の中央点(No.1+10)は、以下の式で算出することができます。

M2＝M1÷4

つまり、

M1＝2.0mとすると、

M2=M1÷4

　＝0.5m

となります。

このように、難しい座標計算をすることなく、単曲線の中間地点を算出する方法が土方カーブです。

土方カーブの公式

実際にどのように土方カーブを用いるのかわかったところで、土方カーブの公式を紹介します。

土方カーブの公式

M1≒(C^2)/8R
M2=M1/4

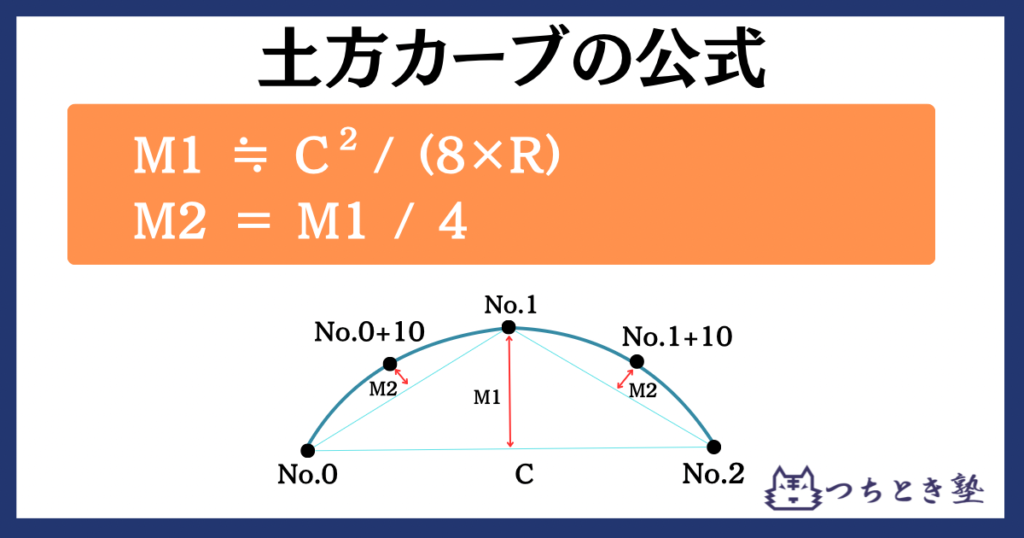
この図のように、既知の情報から、簡単な四則演算で単曲線の中間地点を算出することができます。

土方カーブを現場で用いた事例3選

土方カーブは、丁張を用いるような土工事の現場で使用します。

土方カーブの使い方について、理解を深めるために、具体的な計算事例を3つ紹介します。

・単曲線の3点が既知であり、その中間の位置を算出したい場合
・単曲線の半径及び単曲線の2点が既知であり、中間地点を算出したい場合
・単曲線の3点が既知であり、半径を求めたい場合

単曲線の3点が既知であり、その中間の位置を算出したい場合

単曲線上の既知点3点から、 その中間点の位置を算出する方法です。

計算方法

①CとM1 を計測する
②M1÷4 より M2 を計算します

計算により求めたM2 を現場に表現することで、 単曲線を表現することができます。
また、さらに細かく位置を出したい場合には、この計算を繰り返すことにより、滑らかな単曲線を表現することができます。

例
M1＝5.0mの場合
M2＝M1÷4
　 ＝5÷4
　 ＝1.25m

単曲線の半径及び単曲線の2点が既知であり、中間地点を算出したい場合

次に、単曲線の半径がわかっている状況で、2点の既知点より、中間点を計算する方法です。

この図のように、2点の既知点に半径が分かれば、中間点を算出できます

計算方法

①計測したCとRよりM1を計算する
②M1÷4よりM2を計算する

例
C:50m、R200m の場合
M1≒(C^2)/8Rより、
　　=(50^2)/(8×200)
　　= 1.5625m

単曲線の3点が既知であり、半径を求めたい場合

最後に半径が分からない場合、 既知点3点から半径を求める方法です。

計算方法

①M1とC を計測する
②M1とCよりRを計算する

といった手順で計算します。

例
C:50m、M1:1mの場合
M1≒(C^2)/(8R) より、R=(C^2)/(8×M1)
R=(50^2)/(8×1)
=312.5m

土方カーブの注意点

現場で簡単に計算できて、測量機器なしで作業ができる土方カーブですが、使用する上で、注意点があります。

・計算が可能なのは基準の中央点のみ
・精度は高いと言えない

それぞれ詳しく解説します。

計算ができるのは基準の中央点のみ

土方カーブは便利な計算ですが、使用できるのは、基準となる点の中央点のみとなります。
その理由は、あくまで四則演算として近似式を用いた公式であるから。

道路土工-施工指針によると、丁張の設置間隔は300m以上の場合、10m であり、延長が300m以下では設置間隔を5mとされています。
そのため、10m 間隔の丁張とすると、まず計算可能な点は10m間隔の中央である 5m です。

そして、5m を設置したあとに、その中央点である 2.5m 及び 7.5m 地点に設置できます。
その他の場所では、土方カーブの計算式を使用できないので注意してください。

【必見】誤差に注意すること

土方カーブを用いる際には、高い精度を要する構造物を構築する際には不向きです。

中央縦線 M1 については、近似値から求めるため、半径が小さい場合、 弦の長さが長くなると、近似値と実測値が大きく異なることに加えて、測量機器を用いないことから、精度は低くなります。

土方カーブは、近似値を用いた式であることに加えて、 測量機器を使用しないため、精度が高いとは言えません。

実際に、弦の長さから近似値で求めた中心縦線 M1は誤差があるので、弦の長さを10m とし、半径を変化させた場合の例を表にまとめました。

弦の長さ(角度)を固定して、半径を変化させた場合

半径	弦の長さ	実測値	計算値
2000m	10m間隔	0.63mm	0.63mm
1000m	10m間隔	1.25mm	1.25mm
500m	10m間隔	25.00mm	25.00mm
100m	10m間隔	125.1mm	125.0mm
50m	10m間隔	2,506mm	2,500mm
10m	10m間隔	13,397mm	12,500mm

このように、 半径が小さくなると無視できない誤差の大きさになります。

次に、半径100m の曲線とし、弦の長さを変化させた場合の例を表にまとめました。

半径を固定して、弦の長さ (角度)を変化させた場合

半径	弦の長さ	実測値	計算値
100m	10m間隔	125.1mm	125.0mm
100m	20m間隔	503.0mm	500mm
100m	30m間隔	1,131.4mm	1,125.0mm
100m	40m間隔	2,020mm(2.02m)	2,000mm(2.00m)
100m	50m間隔	3,175.4mm(3.175m)	3,125.0mm(3.12m)

このように30m間隔で中央点をだそうとすると、無視できない誤差になります。

このように、近似値による誤差に加えて、測量機器を使用しないことによる施工誤差もあるため、許容できる場合に使用してください。

現場で土方カーブを使う際の注意点

土方カーブは現場で簡易的に位置を出すことができますが、注意点があります。
それは、シビアな規格値の構造物を構築する際には適さないということ。

精度が高いとはいえない

例えば、新設の道路を構築する工事では、基準となる点は光波等の測量機器で位置を出し、あくまで最低限必要な部分のみ土方カーブを補助的な要素として用いて下さい。

土方カーブはあくまで補助的手法です。

土方カーブの計算方法【まとめ】

土方カーブの計算方法と現場での利用方法について解説しました。

以上、現場で簡単にRを出す土方カーブについて方法をお伝えしました。