\ 公式LINE登録は完全無料 /
今すぐお友達になる公式LINE限定で、土木施工管理技士試験対策のプレミアム記事を公開中

 若手技術者
若手技術者令和6年度から開始される土木工学の基礎問題はどんな問題が出題されるのか不安だな・・・
本記事では、こんな悩みにお答えします。
土木施工管理技士の技術検定において、令和6年度の試験変更に伴い追加される「土質力学」「構造力学」「水理学」の問題。
1級土木施工管理技士の試験の受験を予定されている方は、どんな対策をすればいいのか不安に感じているかたもいらっしゃると思います。
ですが、1級に先立って、2級土木施工管理技士の試験が6月2日に実施されたことで、出題される問題の傾向が少しは明らかになりました。
そこで、今回は2級で出題された内容の解説と、問題を踏まえて出題されそうな分野について解説します。
1級土木施工管理技士の試験を今年受験される予定の方は、ぜひ最後まで読んでください。

 若手技術者
若手技術者1級を受けるのですが、 工学の基礎知識について
どんな問題が出るのか不安です
 ぜねた
ぜねた2級で出題された工学の基礎の問題について解説しますので、
参考にしてください。
今回、試験制度の変更に伴い新たに、追加で発表されていたのが土木工学の基礎知識。
受験資格において、実務経験が問われなくなった代わりに、土木工学の知識を有しているかどうかは、試験の問題で問われるようになりました。
しかしながら、どんな問題が出題されるのかは未知数でしたが、先日、6月2日に2級の試験が実施されたことで、試験に問われるレベルが明らかになりましたので、解説します。
なお、2級の試験で今年から出題された5問はすべて必須回答の問題でした。
令和6年度における2級の試験で出題された問題
①土の構成から土粒子の密度を表す式を示す
②粒径加積曲線から土の粒形を読みとる問題
③単純梁の断面二次モーメントに関する問題
④図心に関する問題
⑤開水路の流量の計算方法
それぞれ詳しく解説します。
まずは、問題をみてみましょう。
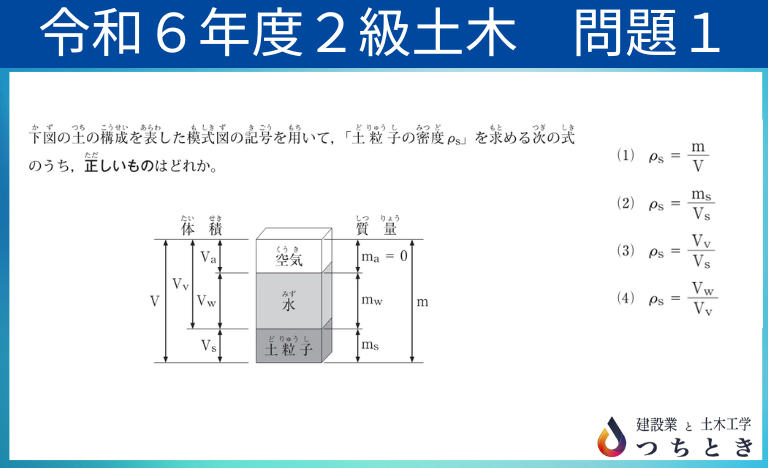
①土の構成
今回は、土の模式図を理解できるかが問われていて、土粒子の密度を表す式は何かという問題でした。
ρs=ms/Vs
ρsは土粒子のみが空間を満たした状態における単位体積重量です。
一般的には、2.65~2.70g/c㎡の値を示します。
土の構成が分かっていれば、それほど難しくない問題です。 正直、知っているか知らないかです。
今回の内容を受けて1級を受験予定の方が対策するなら、
他にも、
体積に関する物理量として、間隙比、間隙率、飽和度や、
質量に関係する物理量として、土の湿潤密度、乾燥密度、飽和密度といった
基本的な式と式の意味について勉強しておくべきかなと思います。
まずは問題です。
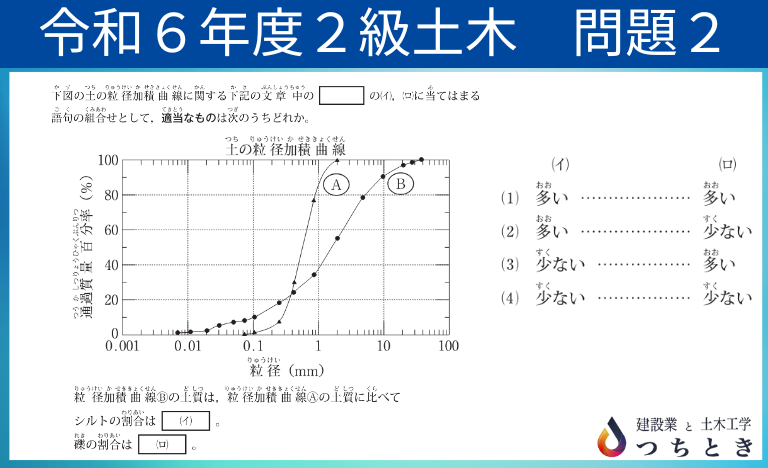
②粒径加積曲線
出題された問題は、粒径加積曲線のグラフが2つあり、そこから「シルト」と「礫」の割合がどう違うかを答える問題でした。
この問題に回答するためには、2つの知識が必要です。
・粒径と土の種類の関係性
・土の粒径加積曲線の読み方
まずは、粒径の分類を覚えましょう。
・粘土 0.001~0.005mm
・シルト 0.005~0.075mm
・砂 0.075~2mm 2~10mm
この部分は正直に言って覚えるだけです。
次に、粒径加積曲線の読み方について解説します。
粒径加積曲線は、土粒子の粒形を横軸に対数目盛で示し、縦軸に通過百分率で示したグラフです。
土の粒形加積曲線を描くことができると、その土に含まれる粒子の大きさの相互関係を知ることができます。
先ほどの粒形と合わせると、以下の図の通りです。
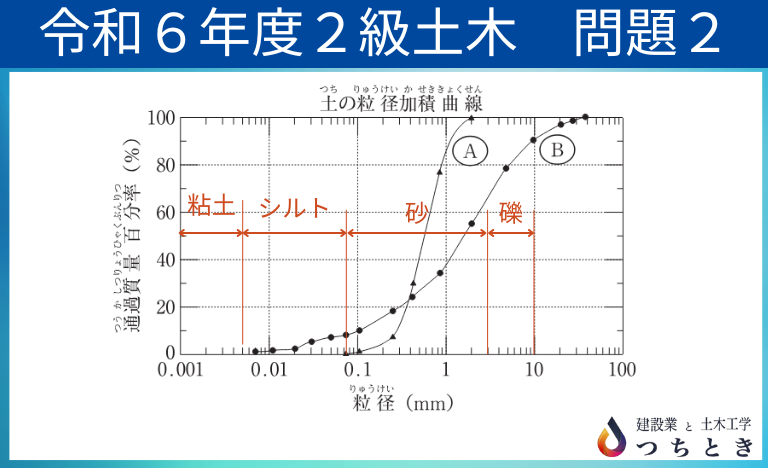
では、実際の問題を見てみましょう。
以下の土の粒径加積曲線のグラフから、曲線Bと曲線Aそれぞれのシルトと、礫の割合を読み取ります。
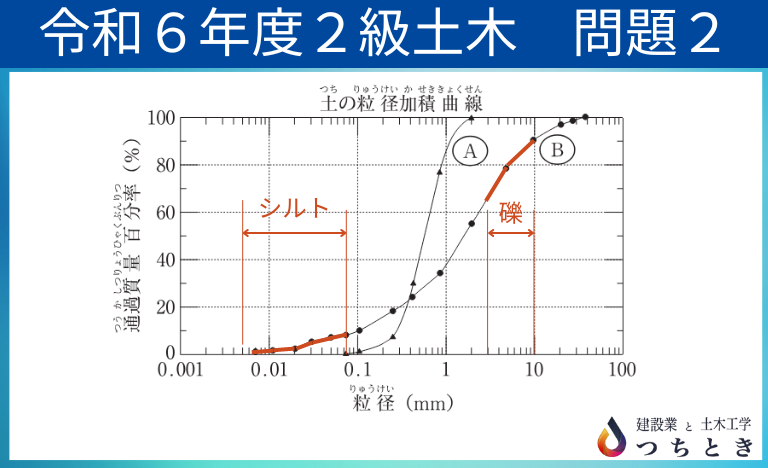
通過質量百分率
| A | B | |
|---|---|---|
| シルト (0.005~0.075mm) | ほぼ0% | 0~10% |
| 礫(2~10mm) | ほぼ100% | 55-90% |
となります。
つまり、Bはシルト分が10%で、礫は35%となります。
Aはシルト分が0%で、礫も0%となります。
といったことを粒径加積曲線から読み取ることができます。
まずは、問題を見てみましょう。
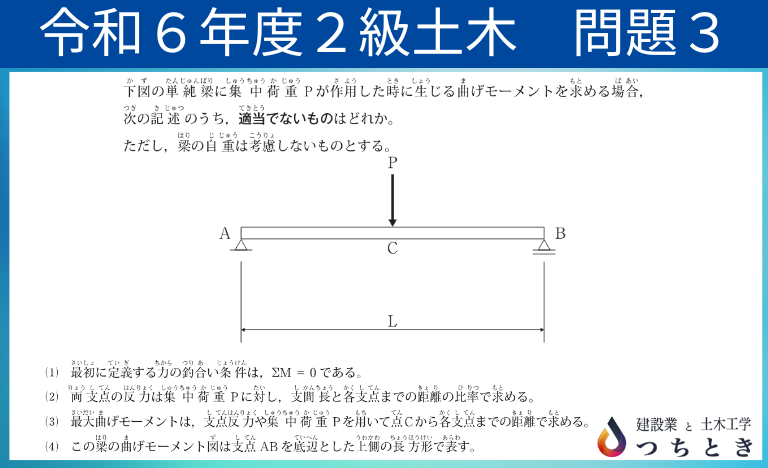
単純梁に集中荷重が作用した場合に生じる曲げモーメントを求める問題です。
単純梁の曲げモーメントを求めるまでの流れがわかれば、解答できる問題でした。
まずはこの図に働く力のつり合いを分解します。
物体が静止している条件として、
・鉛直方向及の力が釣り合っている (ΣY=0)
・水平方向の力が釣り合っている(ΣX=0)
・モーメントが釣り合っている (ΣM=0)
水平方向に働く力はないので、鉛直方向の力のつり合いを考えます。
鉛直方向の力のつり合いは、
RA+RB=P
となります。
各支点における反力を足したものが、外力Pと同じです。
なお、集中荷重Pの作用する位置を、以下の図であらわすと、
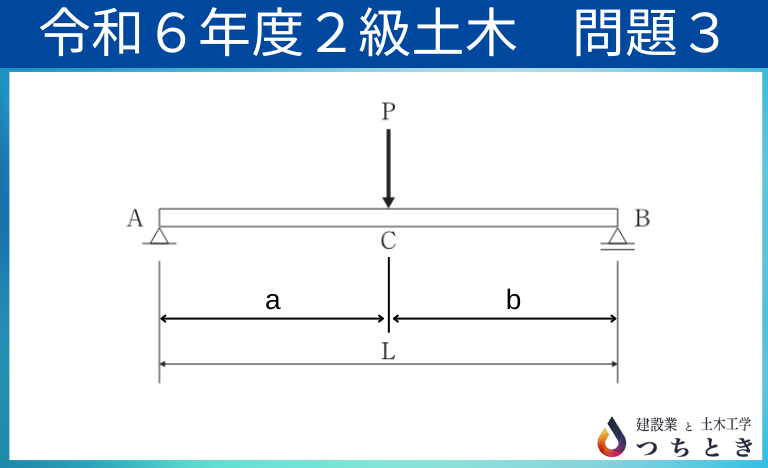
となり、
単純梁の鉛直方向の反力は 、
RA=P×b/L
RB=P×a/L
です。
そのため、支点の反力は支間長と各支点までの距離の比率であらわすことができます。
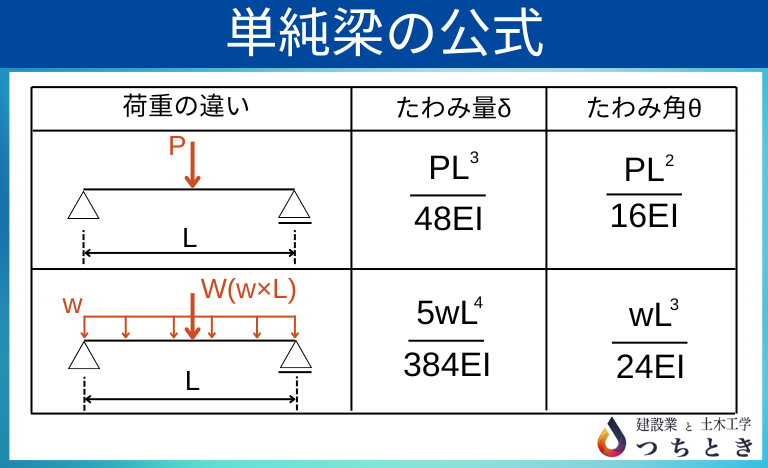
また、単純梁におけるせん断と曲げモーメントは以下の図を覚えてください。

M図は集中荷重が作用するまでの位置に関する1次関数です。
そのため、せん断図の符号が正から負へ変わる位置で曲げモーメントが最大になり、三角形のカタチになります。
こちらも公式の暗記と、公式の意味を理解していれば、解ける問題でした。
1級に向けて勉強をするのであれば、単純梁の曲げモーメントを求めるまでの流れに加えて、せん断図、曲げモーメント図の理解までは押さえておきましょう。
そして、等分布荷重の場合まで覚えて私だったら押さえておきます。
そして、等分布荷重と集中化準まででも、変位(たわみ)の公式まで覚えていれば十分かと思います。
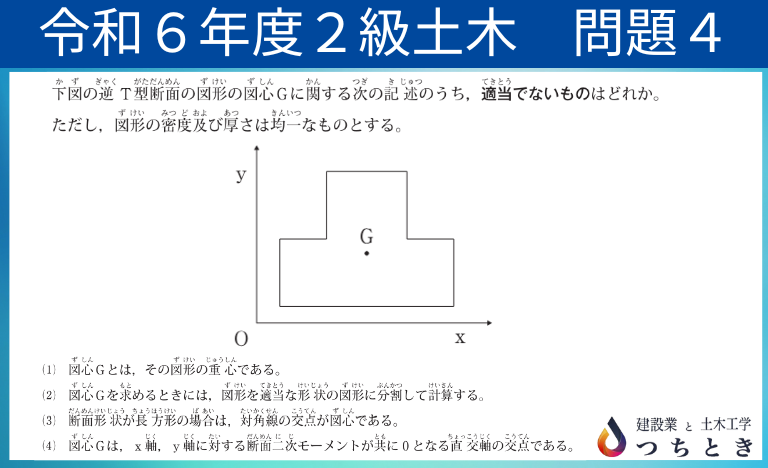
逆T型断面における図形の図心を求める問題です。 図心を求めることができれば、解答できる問題でした。
そもそも図心とは、その位置を支点にしたとき力が釣り合う点です。
図心の計算方法は、長方形のカタチであれば対角線の交点になります。 これが基本です。
複雑なカタチであれば、長方形に分割して各々図心と面積から考えることができます。
例として、先ほどの問題に数値を入れて計算してみましょう。
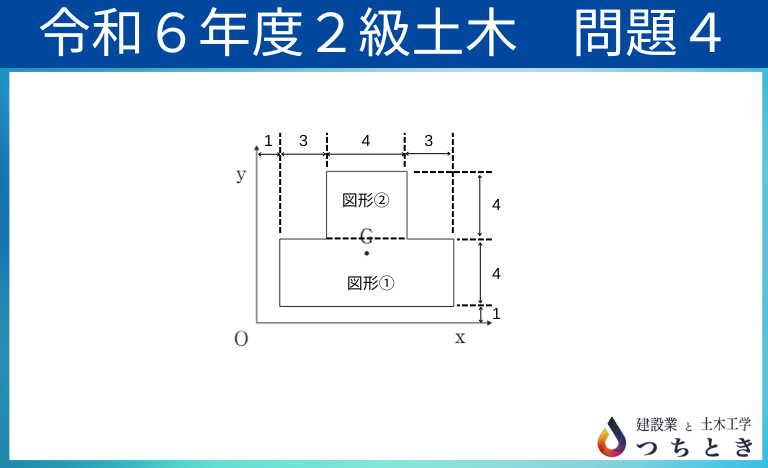
図心の位置を求める計算式は、以下のとおりです。
Σ(Axy) / ΣA
それぞれの図形に分けて計算します。
①の図形は、
A × y=10×4×3=120
②の図形は、
A × y=4×4×7=112
全面積は、
A=4×10+4×4
=56
となります。
y=(120+112)/56
=4.14
となり、下から4.14の位置が図心です。
なお、X方向に関しては、図形の中心であるため割愛します。
また、断面一次モーメントは図心を求めるときに利用されるので、覚えておきましょう。
まずは、問題を見てみましょう。
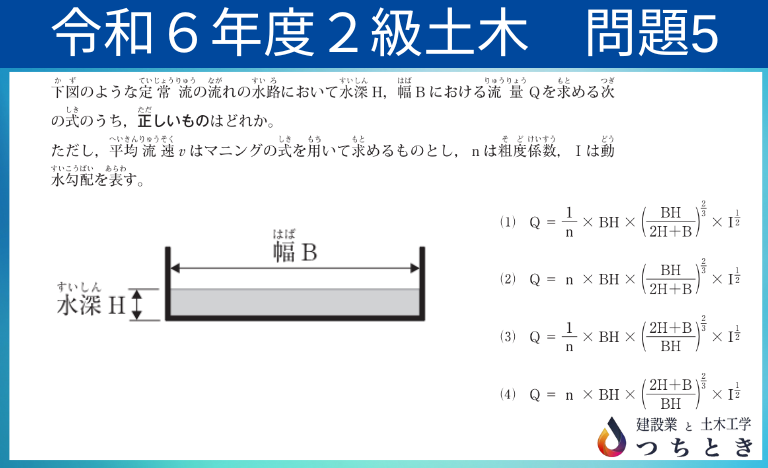
定常流れの開水路における流量を求める問題です。
開水路における流量の計算式と、径深の計算が分かっていれば、解答できる問題でした。
まず、開水路における流量の計算は、Q=AVで計算できます。
この時の流速Vは、マニング公式により求めます。
V=(1/n)× R (2/3)×I(1/2)
n: 租度計数
R: 径深
I : 導水勾配
で求めることができます。
つまり、先ほどの図の場合、 径深Rを求めることができれば、速度を求めることができます。
開水路の矩形断面の場合、以下の式で径深を求めます。
径深R= (BH)/(B+2H)
B:幅
H:高さ
となります。
そして、流量の式に
A=BH
を代入すると、
Q=(1/n)×BH× (BH/2H+B) (2/3)×I(1/2)
となります。
以上が令和6年度から追加された土木工学の基礎知識に関して、2級土木の問題を解説しました。
1級土木の受験を予定されている方の参考になれば幸いです。
ちなみに、 ぜねた公式LINEでは、 土木施工管理技士に関する最新の情報を公式LINE 内限定でお届けしています。
 ぜねた
ぜねた今後、経験記述の書き方に関する電子書籍の配布を予定しています
さらに、数名限定としますが、 経験記述の添削サービスも展開していこうと思いますので、ぜひ見逃さないようにお友達登録をお願いします。

参考
一般社団法人 全国研修センター
https://www.jctc.jp/mondai/
図解を使用される際には、必ず以下のリンクを出典元としてご記載をお願いします。
<利用条件>
1 情報の出典元として「つちとき」の明記をしてください
2 WEB上で使用する場合は、出典元として以下のリンクを設置してください
(https://doboku-koji.com/reiwa6-2kyudoboku)
(nofollow属性不可)

この記事が気に入ったら
フォローしてね!
『つちとき』にコメントする