【エクセルあり】ヘロンの公式とは！？三角形の面積を計算する方法！土木11年のプロが解説

建設工事でよく使用するヘロンの公式って便利ですが、計算式ってなかなか覚えにくいですよね。
現場で関数電卓を叩いて、ささっと計算できる先輩を見て、「カッコいい」と思っていましたが、式をなかなか覚えられずに苦労しました。

実際に使用する機会は多いので、事務所に戻らなくても計算できるのでしっかりと覚えましょう。

本記事では、“ヘロンの公式”の解説に加えて、実際にどうやって計算するのか計算例を交えて解説します。
また、実務で使用できるエクセルシートもダウンロードできるように公開しているので、良かったら活用してください。

執筆者

『つちとき』管理人｜元準大手ゼネコン勤務｜土木の現場監督7年｜１級土木施工管理技士｜書籍『仕組み図解 土木工事が一番わかる』著者

『つちとき』管理人｜元準大手ゼネコン勤務｜土木の現場監督7年｜１級土木施工管理技士｜【経験工種類】道路土工事、トンネル、PC上工、橋梁下部工｜書籍『仕組み図解 土木工事が一番わかる』出版

当サイトの運営者ぜねたの詳しいプロフィールは、コチラです。

あわせて読みたい

当ブログについて 当サイトの管理人である元ゼネコンマンのぜねたです。 土木の魅力について発信しています。

また、水準測量の計算方法については[水準測量の計算方法はこれでバッチリ!野帳の書き方を現場監督7年の土木技術者が解説]で詳しく解説しています。

あわせて読みたい

【プロが語る】水準測量の野帳の書き方！計算方法を徹底解説 この記事では、水準測量の計算方法について解説しています。野帳の書き方が気になっていた方にもおすすめの記事です。

【ヘロンの公式】エクセルシート

実務で使用できるヘロンの公式の計算式を入力したエクセルシートを共有します。

ダウンロードして活用してください。

面積の計算結果は、小数点第3位で切り捨てになっているので注意してください

＼　面積の計算もこれでラクラク　／

ヘロンの公式とは？三角形の面積を計算する公式

若手技術者

公式を教えてください。

ぜねた

「A(面積)＝√s(s-a) (s-b) (s-c)」 と 「s=(a+b+c)/2」 の2つの式から面積を算出します。

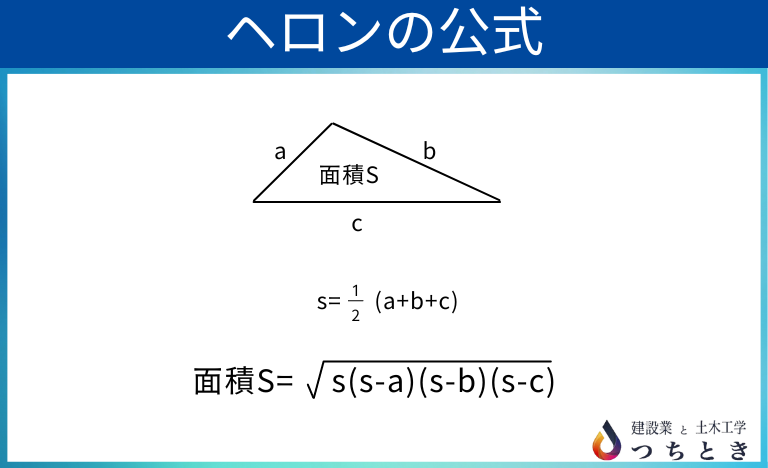
土木の工事でよく使う「 ヘロンの公式」は三角形の面積を計算する公式で、 3辺の長さが分かることにより面積が計算できます。

まずは、公式を解説します。

この三角形で面積を計算する場合、 ヘロンの公式だとどのように計算するのか解説します。

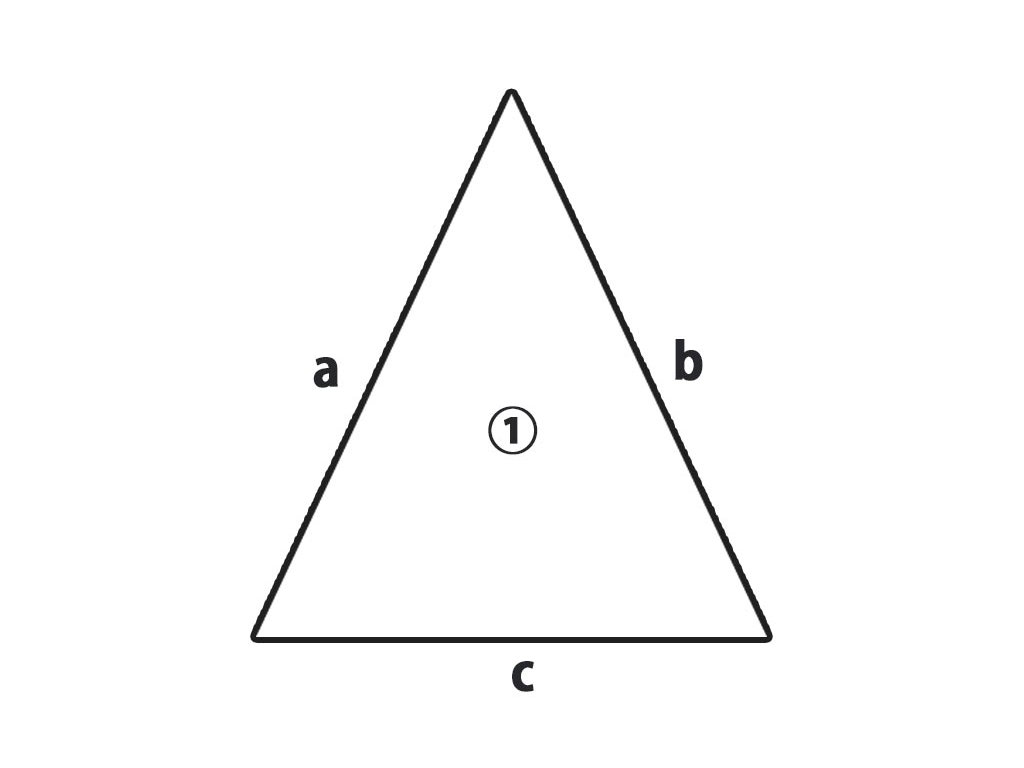
公式は以下の通りです。

A (面積) =√s(s-a) (s-b) (s-c)
s=(a+b+c)/2

まず最初に sを計算したあとに、面積を計算します。

ヘロンの公式を使用する理由

なぜ、ヘロンの公式を使うのか?

というと、

三角形の3辺の長さが分かることで面積を算出できるというのは、非常に汎用性が高いからです。

ぜねた

現場の出来高を測定する際には、よく使用されます。

特に、舗装工やのり面工事、用排水河のシールコンなど、凸凹した面でも面積を計算できるので重宝します。

次に、実際の計算例を解説していきます。

ヘロンの公式を使った計算例 ①

このような三角形を計算したい場合

a=3.55m、 b=4.21m、c=5.11m

とすると、

s=(3.55+4.21+5.11)/2
=6.44
A=√6,44× (6.44-3.55)×(6.44-4.21)x (6.44-5.11)
=7.39

という計算になります。

結果を以下の表にまとめます。

ヘロンの公式を使った計算例②

このような形の面積を測りたい場合を例として解説します。

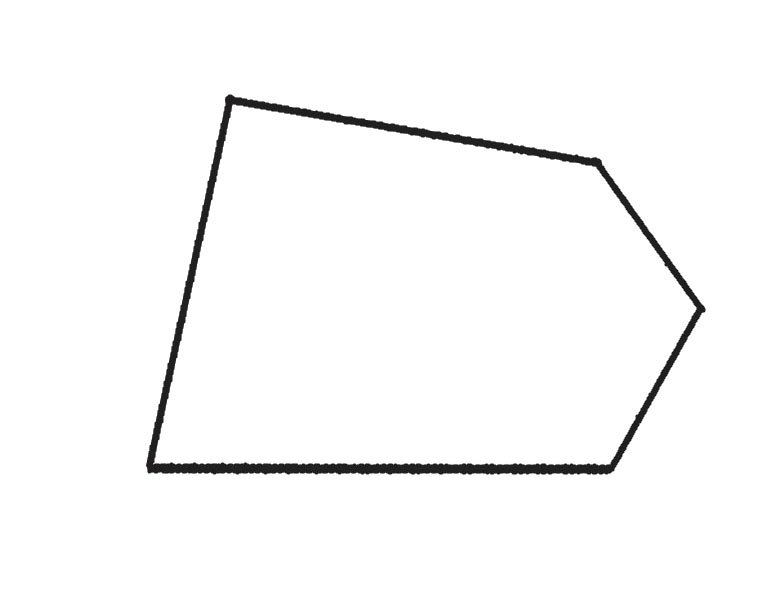
まずこの図形を3角形に分割します。

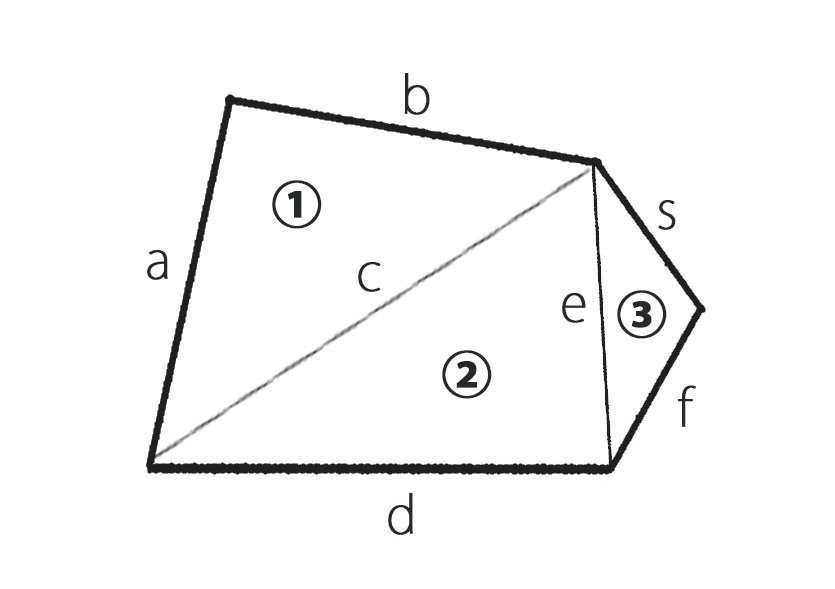
この図のように分割した場合、

a=4.48m、 b=4.47mc=7.21m、d=7.44m、e=5.01m、 f=2.57m、g=3.93m

とすると、

面積を計算する場合は、3角形に分割して計算します。

①の三角形
s①= (4.48+4.47+5.21)/2
=8.08
A① = √8.08×(8.08-4.48)×(8.08-4.47)×(8.08-5.21)
=9.55

②の三角形
s②=(7.21+7.44+5.01)/2
=9.83
A②=√ 9.83× (9.83-7.21)×(9.83-7.44)×(9.83-5.01)
=17.22

③の三角形
s③=(5.01+2.57+3.93)/2
= 5.76
A③=√5.76× (5.76-5.01)×(5.76-2.57)×(5.76-3.93)
=4.99

A=A①+A② +A③
=9.55+17.22+4.99
＝31.76

と計算できます。

計算する場合の注意点

エクセルを使って計算する際の注意点を解説します。

ポイントは一つ。

ぜねた

少数点以下の何桁まで使って計算するのか、要注意です。

どこの段階で四捨五入するのかで最後の面積が変わります。

公共工事では、面積は小数点2桁で計算するのが一般的です。

例 sを小数第三位で四捨五入した場合

例 sを小数点3桁以下で切り捨てにした場合

このように、sで切り捨てと四捨五入で場合で、sとAが変わります。

ぜねた

私個人の経験からすると、sは小数点3桁を四捨五入して、面積を計算するときには3桁を切り捨てるのが一般的です。

s=(3.55+4.21+5.11)/2
=6.435
A=√6,44× (6.44-3.55)×(6.44-4.21)x (6.44-5.11)
=7.398099….

以下の結果を表にまとめると以下の通りです。

【まとめ】ヘロンの公式

土木工事において必須の、「ヘロンの公式」について解説しました。

ヘロンの公式を使った面積の計算方法が理解できたと思います。

以上、ヘロンの公式について解説した。